Alright, so check it out, today I’m gonna break down this little coding challenge I tackled: “total points in a volleyball game.” It wasn’t rocket science, but it got me thinking, and that’s always a good thing, right?

So, it all started when I saw this question floating around. The basic idea is: you’ve got two teams playing volleyball, and you need to figure out the maximum and minimum possible total points scored in the whole game, given the final score of the winning and losing teams.
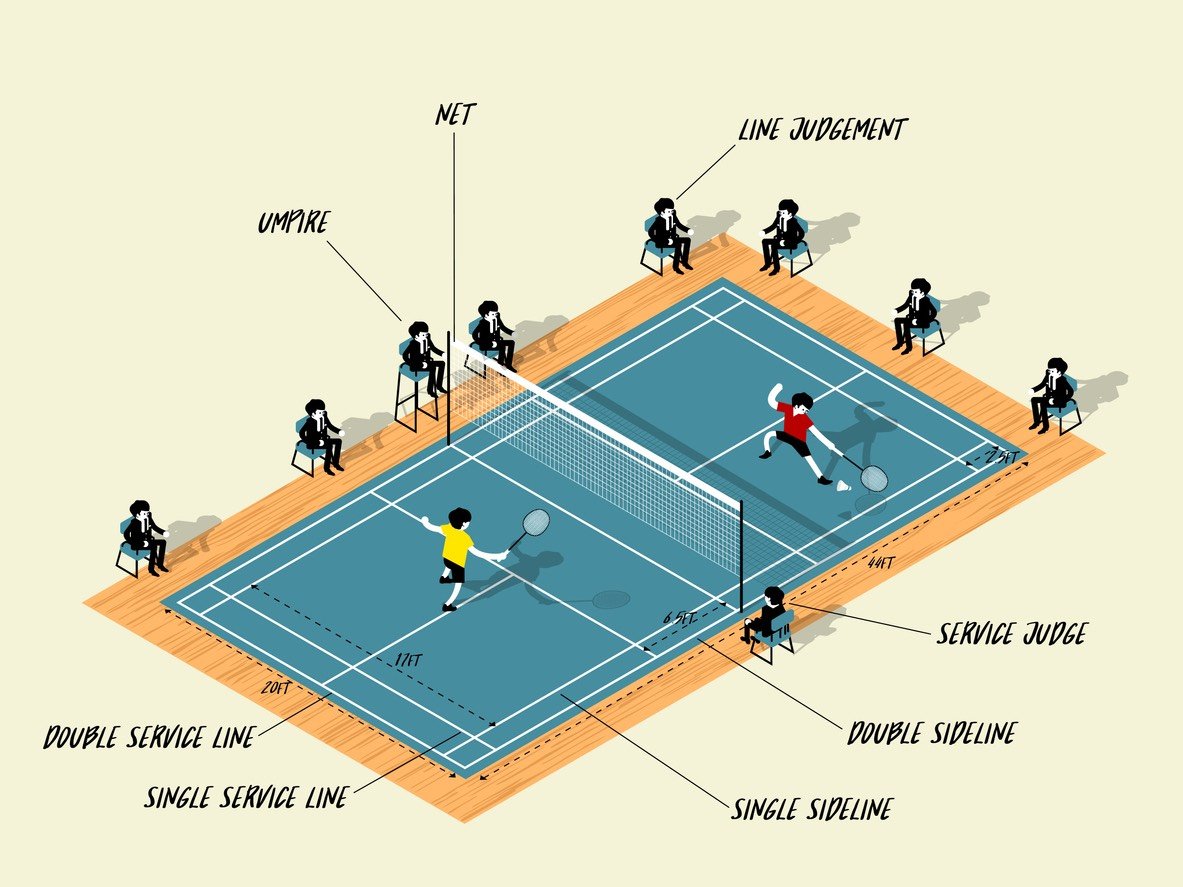
First things first, I had to wrap my head around the rules of volleyball. I mean, I’ve watched it, but I’m no expert. Here’s what I remembered (and looked up to confirm):
- A team needs to score 25 points to win a set (except the final set, which only needs 15).
- A team must win by at least 2 points.
- A match is usually best-of-five sets.
Okay, with that sorted, I started thinking about how to approach the problem. It’s basically about figuring out how many sets were played and what the scores could’ve been in each set.
The Minimum Possible Points:
This is where I started. To minimize the total points, you want to minimize the number of sets played. The fewer sets, the fewer points scored overall, obviously.
So, if the winning team’s score is w and the losing team’s score is l, if w and l fulfill the conditions to win by minimum sets(3 sets) then the minimum points will be the sum of all scores.
But if the sets are 4 or 5. Then the sum points will change accordingly.
The Maximum Possible Points:
This is where things got a bit trickier. To maximize the total points, you gotta maximize the number of sets played and also ensure that the losing team scores as many points as possible in each set without actually winning.
The maximum score happens when there are five sets played, and the point difference is always 2 points.
Coding it Up:
Once I had the logic down, I started banging out some code (in Python, of course – my go-to for quick stuff like this). I won’t bore you with all the details, but here’s the gist:
- I created functions to calculate the minimum and maximum points based on the winning and losing scores.
- Inside those functions, I considered all the possible scenarios: 3 sets, 4 sets, or 5 sets.
- I handled the edge cases where the winning score was exactly 25 (or 15 in the final set) and the losing score was just below that, ensuring the 2-point win condition was met.
Testing, Testing:
Of course, I didn’t just write the code and call it a day. I threw a bunch of test cases at it to make sure it was working correctly. I tried different winning and losing scores, different numbers of sets, and even some crazy edge cases to see if I could break it. Luckily, it held up pretty well!
What I Learned:
This little exercise was a good reminder that even simple problems can be surprisingly nuanced. It forced me to think through the rules of volleyball carefully and to consider all the different possibilities. Plus, it was a fun way to sharpen my coding skills. Now, if you’ll excuse me, I’m gonna go watch some actual volleyball. Maybe I’ll even understand what’s going on this time!